EMpy

Single Layer Anti-Reflection Coating

The isotropic transfer matrix algorithm can be used to study anti-reflection coatings. A very simple single layer anti-reflection coating, described here, is computed by the following script.

In the lines 8-12 the multilayer is defined. Indices and thicknesses are chosen so that a single layer of refractive index 1.38 and thickness about one quarter of the central wavelength 1.55um is positioned between two semi-infinite layers of air and glass. This gives theoretically no reflection for the central wavelength. The following graph is the result, which confirms the theoretical predictions.

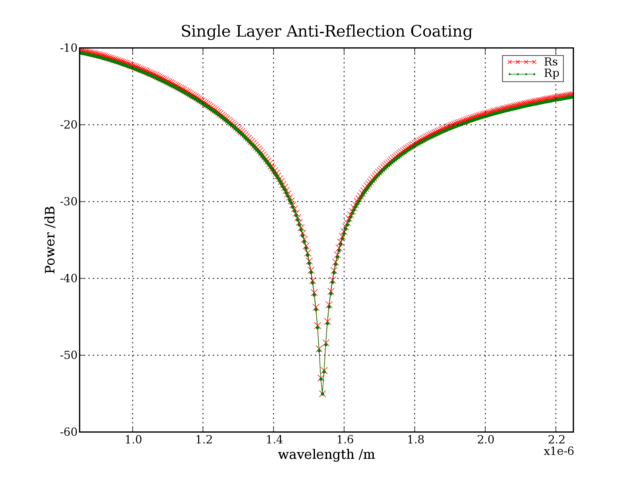
The graph shows two curves, one for each polarization. They differ because the incident plane wave is tilted by 10 degrees (line 15).

back to examples

Anisotropic Multilayer

The anisotropic transfer-matrix can be used to study the following example. The result is shown in the following graph.

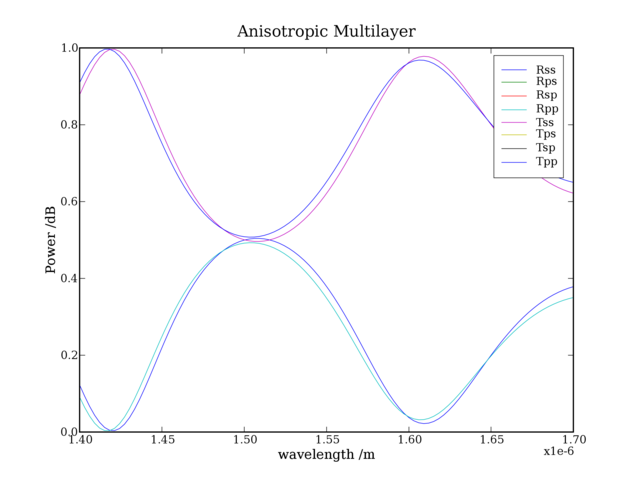
Four curves are clearly visible because the two polarizations behave in a different way, even if the incidence is normal (line 16-17), because of the anisotropic material (line 5).

back to examples

Single Ring Resonator

This is the script to study a single ring resonator:

In lines 4 and 5 the two coupling coefficients and the two coupler losses are defined. The length of the ring is defined in line 6, while its effective index is supposed to be the one of a silicon rib waveguide of 488nm x 220nm at room temperature.

This is its spectrum:

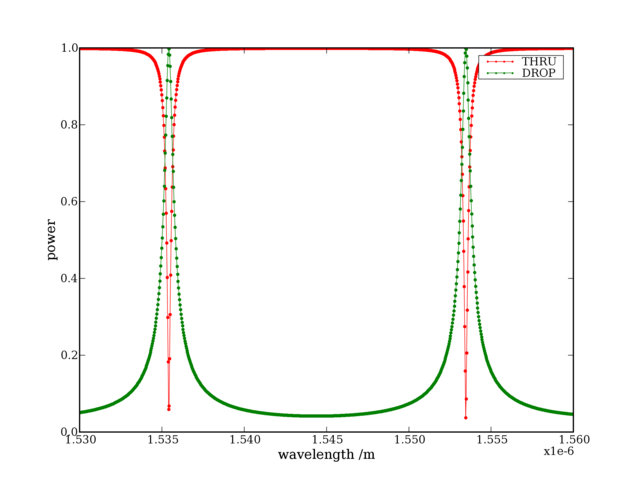
The maximum drop power is 0 dB because no losses are considered, and periodic with the period being the FSR of the ring.

back to examples

N-Rings Resonator

This is the script to study a ring resonator made of 3 rings:

After the "imports", a list of couplers is defined: four, in this case, because the resonator is made of 3 rings. Then, the arcs connecting the resonators are defined: the rings are supposed to be all equal, and the couplers are on the diameters of the rings. Finally, the rings are supposed to have an effective index equal to a 400nm x 200nm straight waveguide, at 125 degrees.

This is its spectrum:

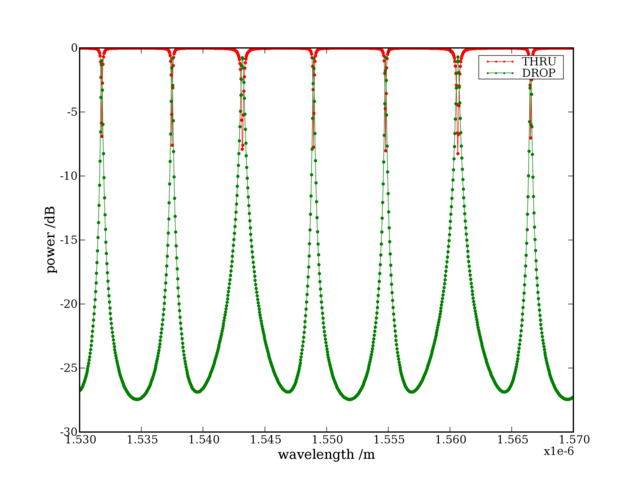
The drop is always lower than 0 dB because the coupling coefficients are not optimized.

back to examples

Finite Difference Fully Vectorial Modesolver

This is the script to find the first two modes of a channel SOI waveguide:

This is a screenshot of the first (TE) mode:

back to examples

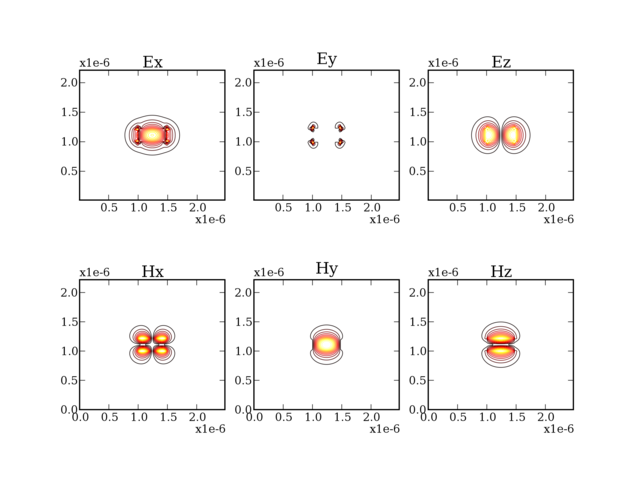
Multilayer with grating

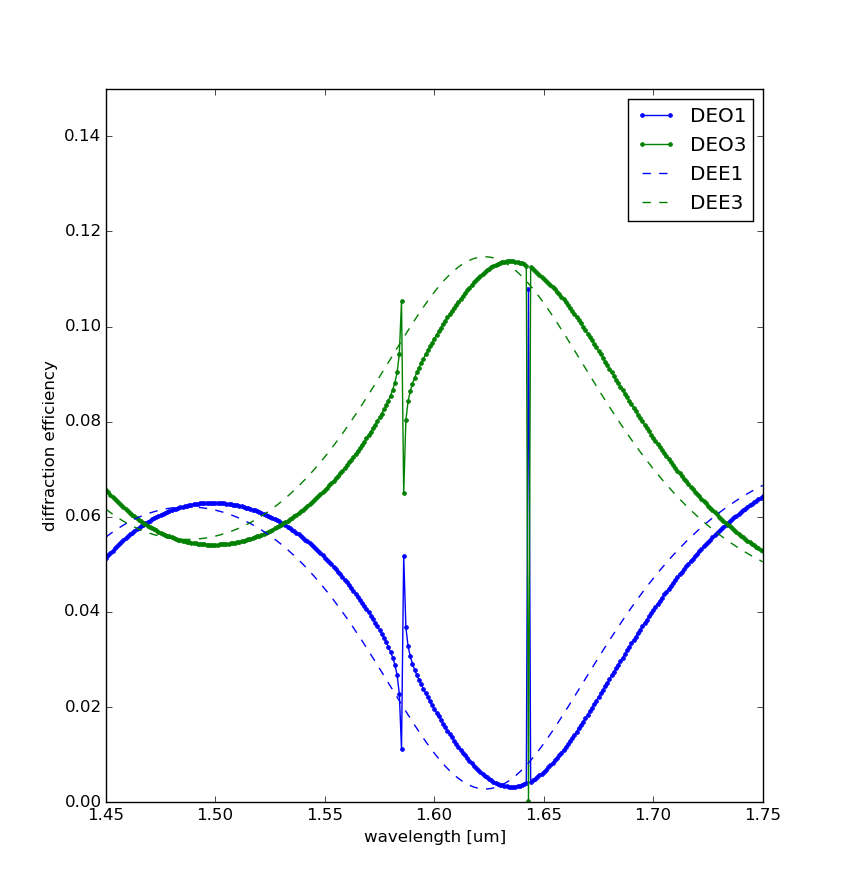
This is the script to study the reflectivity of a grating embedded in an anisotropic multilayer. The multilayer is made of 7 layers, the 4th being a binary grating made with an anisotropic (SiN, rotated with the optical axis not aligned with the coordinate axis) and an isotropic (BPTEOS) material. Incidence is not normal. A comparison of the reflectivity is made with a similar multilayer, where the grating layer has been substituted by an "effective" isotropic layer.

The reflectivity are shown in the picture below (in dashed lines is the reflectivity withouth the grating): the effect of the grating is clearly visible as a peak in the reflectivity.